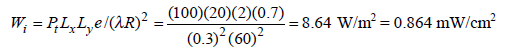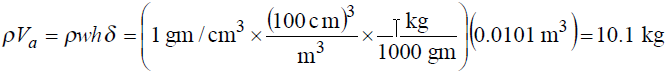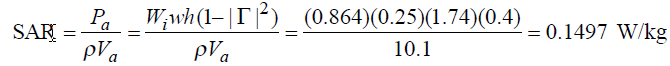Related news
Electromagnetic radiation hazards
ELECTROMAGNETIC RADIATION HAZARDS: Electromagnetic radiation hazards energy is absorbed by the body and deposits energy internally leading to thermal loads and temperature gradients. Since the 1950s the informally accepted tolerance dose in the US has been 10 mW/cm2. The American National Standards Institute (ANSI) officially adopted 10 as the standard in 1966 for a five years term, and it was reaffirmed again in 1969 and 1974. It was concluded at the time that power densities in excess of 100
were needed to produce any significant biological changes.
Also, Power density needed for C temperature increase at 2.45 GHz and 60 minutes.
Later studies revealed that certain body organs were more susceptible to the effects of electromagnetic heating than others. The testis power density safety curve assumes damage when the temperature increases by 1.4 degrees C (which is less than a warm bath).
c=”https://www.mnowaves.com/wp-content/uploads/2020/10/2020-10-24_14-37-25.png” alt=”ELECTROMAGNETIC RADIATION HAZARDS MNO – Engineering Company Design and high quality production of antennas and passive telecommunication parts” width=”436″ height=”289″ />
>> Electromagnetic radiation hazards Effects other than those due to heating have been alleged:
changes in hormone levels, blood chemistry, neurological function, growth, etc. The vast majority of studies have been negative. Research on the effect of EM radiation on the immune system has been inconclusive.
The specific absorption rate (SAR) is used in dosimetric applications:
SAR=σρ
where r is the mass per volume . SAR is the time rate at which electromagnetic energy is imparted to an element of the mass of a biological body.
A linear rise in temperature ΔT can be converted to a SAR value by the formula:
SAR = Δ
Δ
where c is the specific heat of the material
and Δt is the duration
.
It was also found that the body has a resonance when the height (head-to-toe length) is approximately 0.4λ and the electric field is parallel to the body axis. This occurs around 70 MHz for the <span style=”text-decoration: underline;”>standard man (175 cm). Absorption can increase by a factor of seven at resonance.
Summary of current ANSI standards for exposure to non-ionizing radiation
Also, Electromagnetic radiation hazards Data has shown that a whole-body averaged SAR of 4 W/kg is acceptable, and subsequently the standard was set at 0.4 W/kg to incorporate an order of magnitude safety factor. The standard allows the spatial peak SAR to be greater than the whole-body averaged SAR by a factor of 20. Essentially this allows relaxation of the power density limits for partial body exposure. The maximum permissible exposure (MPE) in the 1 to 3 GHz range is based on a 6 minute averaging time.
The safety issue has four aspects:
1) Firstly: The whole-body averaged SAR should be less than the safe level (4 W/kg)
The whole-body averaged SAR is computed taking the average power absorbed by the body over a 6 minutes interval and dividing by the total body weight.
2) Secondly: The maximum partial-body SAR should be less than 20 times the whole-body averaged SAR (80 W/kg)
Partial-body SAR is permitted to be up to 20 times larger than the whole-body averaged SAR. It is determined by averaging over a volume exposed to the strongest incident power density. The appropriate averaging volume is still the subject of discussion. Cubes of 1
, 10
, and 100
have been suggested.
3) Meanwhile: The power density versus exposure time should remain below the safe values for sensitive organs such as the eyes and testes.
“text-align: justify;”> The traditional safety standard of 10 applies to an indefinite time of exposure. It has been recognized that much higher levels are tolerable over short time periods. The most sensitive organ is the testes and the curve shown previously is based on the time and power density to reach
, which is considered potentially dangerous. However, this temperature is exceeded in a common hot bath and thermal-induced damage is generally reversible.
Irreversible injury to the human eye can occur when the exposure reaches several hundred and there are multiple exposures of several minutes in duration. Extended exposures in excess of 10
but less than 300
can cause reversible injuries.
4) Finally: The incident power density must be low enough to avoid a shock or burn hazard.
Current induced in the body can potentially lead to shock if contact is made with a conducting object.
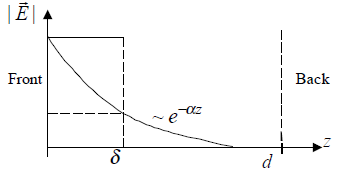
The depth of penetration into and subsequent absorption of a wave by the body are determined by the relative dielectric constant (ε) and conductivity (σ) of the body tissues. These are shown as a function of frequency. The absorption of energy is determined by the attenuation
constant, α.
Because the body is a good conductor, the skin depth is δ≈1/α. The relatively large ε and σ of the body result in a significant reflection of the incident wave at the body/air boundary.
/> />> />>> />c=”https://www.mnowaves.com/wp-content/uploads/2020/10/2020-10-24_18-37-12.png” alt=”” />
Historical note on the industrial, scientific, and measurement (ISM) band (2.45 GHz):
The small skin depth at 2.45 GHz implies that the energy transfer between the wave and body occurs near the surface, and at these shallow depths, the heat exchange mechanisms of the body are effective. Note that this is not a good frequency range for dosimetric (medical) applications because it is difficult to deposit energy deep into the body. The choice of the 2.45 GHz frequency for medical use was based on the erroneous conclusions of data collected by MIT in 1946.
>> The study found that the absorption of water was 7000 times greater at this frequency than at the previously used 27 MHz and it was assumed that the therapeutic heating value would be much greater. Thus 2.45 GHz was adopted as a medical frequency before it was realized that the geometry and electrical properties of the body invalidated the study conclusion.
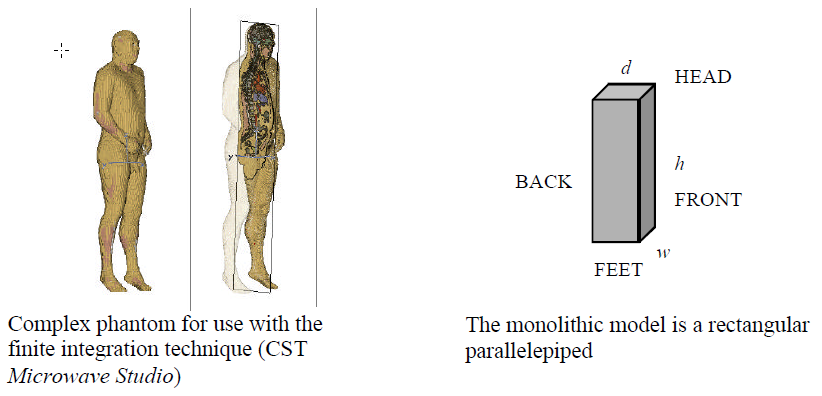
>> Electromagnetic radiation hazards Various models are used in EM radiation and safety calculations. The simplest are spherical and monolithic models of a man. In general, these dummy models are called phantoms.
A sample calculation of whole-body SAR for the monolithic model follows.
Dimensions: height (toe to head), h=1.75 m; width, (across shoulders) w=0.45 m; depth (chest to back), d=0.25 m (volume is 0.1969 ). A height of 175 cm is the standard man.
The densities of fat and muscle are approximately 0.9 and 1.1
, respectively. For convenience, it is assumed that the average density of all body tissues is 1.0
yielding a mass of about 92 kg for the given dimensions.
>> For absorption calculations, the following tissue parameters are used.
| Tissue | σ (S/m) | ε |
| muscle (high water content) | 46 | 2.3 |
| fat (low water content) | 5.5 | 0.15 |
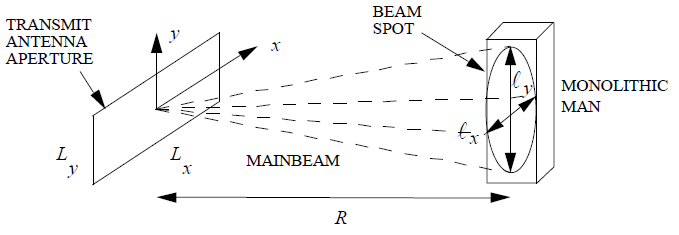
The body is illuminated by an antenna with principal plane beamwidths θ and θ
. At range R the area of the spot is an ellipse with axes
θ
and
θ
. When the spot is larger than the body frontal area, the frontal area is used as the illuminated area; if the spot is smaller than the frontal area, the spot size determines the illuminated area. Therefore the illuminated area of the monolithic body is approximately
π
where
and
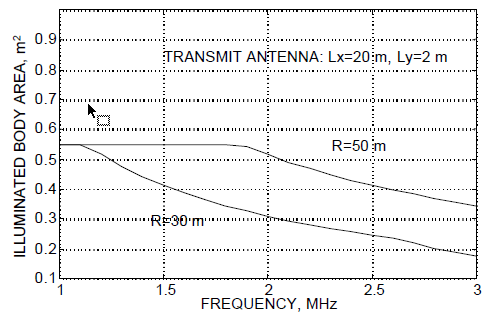
For example, let the aperture dimensions be L = 20m and L
= 2m. Referring to the figure, the spot size at 50 m is greater than the body frontal
area below about 1.9 GHz. Above 1.9 GHz the antenna beam narrows with frequency and less of the body is illuminated. The worst-case whole-body SAR occurs when the spot size is bigger than the body.
For this calculation, it is assumed that all of the incident fields that is not reflected is absorbed: =
Γ
yle=”text-align: justify;”> The reflection coefficient Γ is computed for a homogeneous slab of material (plot shown on p. 8)
η is the intrinsic impedance of the body of thickness d with free space on the backside. The incident power density, assuming the body is in the far-field of the antenna, is:
π
The gain of the antenna with efficiency e is approximately related to the beamwidth by:
G π
λ
≈
π
θ
θ
For this example, another simplifying assumption is that the field in the body is approximately constant within the first skin depth and zero elsewhere. Thus all of the power is absorbed in the first skin depth of the body.
Sample values: P = 100 W, ƒ = 1 GHz, δ = 0.023 m, 1-|Γ|
= 0.4 (from charts on p. 8), R =60 m and e = 0.7. The incident power density is:
which is safe (< 10 mW/cm). For the present case, we use a SAR averaging volume of:
V = whδ = 0.0101 m
.
The heated body mass is:
and the SAR:
which is below the safe level of 0.4 W/kg. The SAR for 1 <em>mW/cm&amp;lt;/em&amp;amp;amp;amp;gt; incident power density is shown at three frequencies and compared to data for other more detailed phantom models
.
<img class=”aligncenter” /&amp;amp;amp;amp;gt;c=”https://www.mnowaves.com//wp-content/uploads/2020/10/2020-10-26_16-58-18.png” alt=”ELECTROMAGNETIC RADIATION HAZARDS MNO – Engineering Company Design and high quality production of antennas and passive telecommunication parts” width=”382″ height=”289″ />
tyle=”text-align: justify;”> <span class=”yoast-text-mark”>=”font-size: 8pt;”>For water c
= 1 cal/gm-
C , r = 1000 kg/m
at 1 atmosphere and 0
, and 1 cal = 4.18606 J.
e=”text-align: justify;”> O. Gandhi, “State of the Knowledge for EM Absorbed Dose in Man and Animals,” Proceedings of the IEEE, vol. 68, January 1980.
Therefore This article retrieved from Professor David Jenn, Naval Postgraduate School, Department of Electrical & Computer Engineering, Monterey, California.
Also you can check our products page.